1-十进制二进制浮点数转换

一、十进制整数->二进制补码

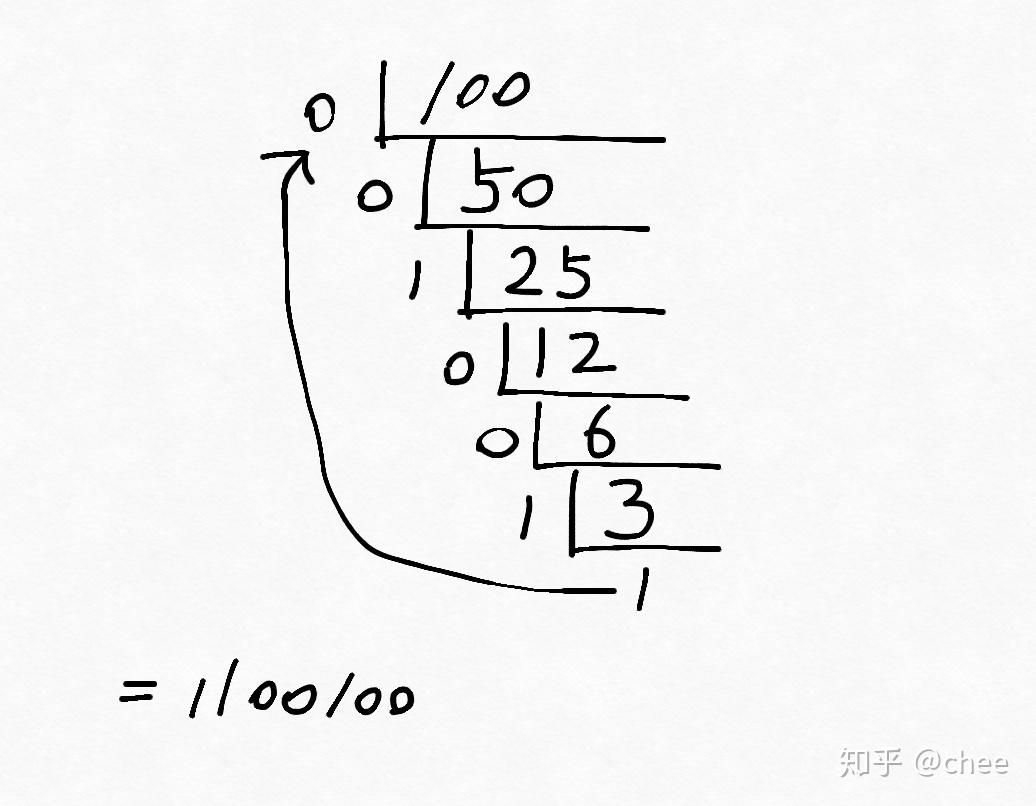
1. 用2整除的方式（正数）

用2整除十进制整数，得到一个商和余数；
再用2去除商，又会得到一个商和余
如此重复，直到商为小于1时为止，
然后把先得到余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，以此排列起来。

2. 负数转化为其补码——（其绝对值转化成二进制后）逐位取反+加一

将负数的绝对值转换为二进制。
对二进制数进行逐位取反（0变1，1变0）。
对取反后的二进制数加1。

3. 将字符数组转换为字符串

1	String binary = new String(binaryStr);

步骤

将字符串转换为整数：

1	int numInt = Integer.parseInt(numStr);

初始化一个长度为32的字符数组，用于存储二进制表示：

1	char[] binaryStr = new char[32];

设置符号位
处理正数：使用除2取余法。从数组的末尾开始填充二进制位。
处理负数：
- 先将负数转换为其绝对值。
- 使用除2取余法，将绝对值转换为二进制表示。
- 对二进制表示逐位取反。
- 对取反后的二进制数加一。注意ifplus
将字符数组转换为字符串并返回

1	String binary = new String(binaryStr);

完整代码：

public static String intToBinary(String numStr) {
    int numInt=Integer.parseInt(numStr);//转成int
    char []binaryStr = new char[32];
    if(numInt>=0){//符号位
        binaryStr[0]='0';
    }else{
        binaryStr[0]='1';
    }
    if (numInt>=0){//正数
        for(int i=1;i<32;i++){
            if(numInt%2==1){//余数是1
                binaryStr[32-i]='1';
            }else{//余数是0
                binaryStr[32-i]='0';
            }
            numInt=numInt/2;
        }
    }else {//负数，等于其正数的二进制数，逐位取反，再加一
        numInt = -numInt;//转正
        for (int i = 1; i < 32; i++) {
            if (numInt % 2 == 1) {//余数是1
                binaryStr[32 - i] = '0';//取反
            } else {//余数是0
                binaryStr[32 - i] = '1';//取反
            }
            numInt = numInt / 2;
        }
        //加一
        boolean ifplus = true;
            for (int i = 31; i > 0; i--) {
                if (binaryStr[i] == '0' && ifplus) {
                    binaryStr[i] = '1';
                    ifplus = false;
                } else if (binaryStr[i] == '1' && ifplus) {
                    binaryStr[i] = '0';
                }
        }
    }
    String binary = new String(binaryStr);
  return binary;
}

二、二进制补码->十进制整数

错误方法-无法通过最大/最小值测试

public static String binaryToInt(String binStr) {
    int num=0;
    if(binStr.charAt(0)=='0'){//正数
        for(int i = 31;i>0;i--){
            int temp=Integer.parseInt(String.valueOf(binStr.charAt(i)));
           for(int j=0;j<32-i;j++){
                temp*=2;
            }
           temp/=2;
            num+=temp;
        }
    }else {//负数
        for(int i=31;i>=0;i--){
            int temp=Integer.parseInt(String.valueOf(binStr.charAt(i)));
            for(int j=0;j<32-i;j++){
                temp*=2;
            }
            temp/=2;
            if(i!=0) {
                num += temp;
            }else{
                num-=temp;
            }
        }
    }
    String numStr=String.valueOf(num);
    return numStr;
}

1.逐位累加（！！从左边开始！！）

逐位累加实现二进制转十进制的过程就是将二进制字符串中的每一位数字（从左到右）根据其所在的位置转换为相应的十进制值，并累加到最终结果中。

从二进制字符串的左边开始，对每个字符进行处理。
对每个字符，计算其对应的二进制值(1/0)，然后将其加到累积结果中。
在处理每个字符时，将当前的累积值乘以 2，并加上当前字符所表示的数字（0 或 1）。

1	num = num * 2 + (binStr.charAt(i) - '0');

这样，最终的结果就是二进制转换成的十进制数。

int num = 0;
if (binStr.charAt(0) == '0') { // 正数
    for (int i = 0; i < 32; i++) {
        num = num * 2 + (binStr.charAt(i) - '0');
    }
}

2. char转int

1	num = num * 2 + (binStr.charAt(i) - '0');

3. 处理负数

逐位取反：将二进制字符串逐位取反。
加一：对取反后的二进制数加一。
累加计算：从第0位到第31位，逐位计算二进制数对应的十进制值。
取反：将结果取负。

注意：二进制负数取反后加一等价于相当于二进制负数先减一，再取反

步骤：

正数处理：
- 从第0位到第31位，逐位计算二进制数对应的十进制值。
- num*2+(dinStr.charAt(i)-‘0’);
负数处理：
- 取反：将二进制字符串逐位取反。
- 加一：对取反后的二进制数加一。
- 累加计算：从第0位到第31位，逐位计算二进制数对应的十进制值。
- 取反：将结果取负。
返回结果：
- 将计算得到的十进制整数转换为字符串并返回。

完整代码

public static String binaryToInt(String binStr) {
       int num=0;
       if(binStr.charAt(0)=='0'){//正数
           for(int i=0;i<32;i++){//从0或者1开始都行，没影响
               num=num*2+(binStr.charAt(i)-'0');
           }
       }else {//负数
          //1. 取反
           char[]binstr=new char[32];
           for(int i=0;i<32;i++){
               if (binStr.charAt(i)=='1'){
                   binstr[i]='0';
               }else{
                   binstr[i]='1';
               }
           }
           //2. 加一
           boolean is_plus=true;
           for(int i=31;i>=0;i--){
               if(binstr[i]=='0'&&is_plus){
                   binstr[i]='1';
                   is_plus=false;
               }else if(binstr[i]=='1'&&is_plus){
                   binstr[i]='0';
               }
           }
           //3. 累加计算
           for(int i=0;i<32;i++){//从0或者1开始都行，没影响
               num=num*2+(binstr[i]-'0');
           }
           //4. 取反
           num=-num;
       }
       String numStr=String.valueOf(num);
       return numStr;
   }

总结：二进制补码和十进制整数相互转换：

负数补码和对应正数补码转换
- 负数转补码：
  1. 将负数的绝对值转换为二进制。
  2. 对二进制数逐位取反（0变1，1变0）。
  3. 对取反后的二进制数加1。
- 补码转负数：
  1. 对补码逐位取反（0变1，1变0）。
  2. 对取反后的二进制数加1。
  3. 将结果int取负。
十进制整数转二进制补码：
- 正数：
  1. 使用除2取余法，从低位到高位依次填充二进制位。
  2. 符号位为0。
- 负数：
  1. 将负数的绝对值转换为二进制。
  2. 对二进制数逐位取反（0变1，1变0）。
  3. 对取反后的二进制数加1。
  4. 符号位为1。
二进制补码转十进制整数：
- 正数：
  - 从第0位到第31位（从左开始！！），逐位计算二进制数对应的十进制值。
- 负数：
  1. 对二进制数逐位取反（0变1，1变0）。
  2. 对取反后的二进制数加1。
  3. 从第0位到第31位，逐位计算二进制数对应的十进制值。
  4. 将结果取负。

三、十进制整数的真值转化成NBCD

1. NBCD

NBCD格式：
1. 符号位
  - 正数：1100
  - 负数：1101
2. 每个十进制数字用4位二进制数表示。
3. 确保NBCD表示一定是32位。
  - 在符号位和有效位之间填充0!

2.将单位十进制数字转化为4位二进制形式

除2取余法
- 先得到的余数作为低位有效位

public static String CharTo4bit(Character character){
    int a = character-'0';
    char[] stringOf4=new char[4];
    for (int i = 0; i < 4; i++) {
        stringOf4[i] = '0'; // 初始化字符数组为'0'
    }
    for (int i = 3; i >= 0; i--) {//转换为二进制[除二取余法]
        if (a % 2 == 1) {
            stringOf4[i] = '1';
        }
        a /= 2;
    }
    return new String(stringOf4);
}

3. 步骤

将字符串转换为整数。
初始化一个 StringBuilder 用于构建NBCD字符串。
根据整数的符号设置符号位：
- 正数：1100
- 负数：1101
计算需要填充的零的数量，以确保NBCD表示是32位。
将每个十进制数字转换为4位二进制形式，并添加到 StringBuilder 中。
返回NBCD字符串。

4. 【注意】语法

return new String(stringOf4);
- 适用于将字符数组char[]转换为字符串的场景
return nbcdStr.toString();
- 适用于将StringBuilder对象转换为字符串的场景

完整代码

public static String decimalToNBCD(String decimalStr) {
    StringBuilder nbcdStr = new StringBuilder();
    int num = Integer.parseInt(decimalStr);
    int length = decimalStr.length();
    int zero_length = 0;
    if (num>=0){
        zero_length=28-4*length;
        nbcdStr.append(1100);//符号位
        for(int i=0;i<zero_length;i++){//填充零
            nbcdStr.append(0000);
        }
        for(int i=0;i<length;i++){
            nbcdStr.append(CharTo4bit(decimalStr.charAt(i)));//转换每个十进制数字,并添加到 StringBuilder 中
        }
    }else{
        zero_length=28-4*(length-1);
        nbcdStr.append(1101);
        for(int i=0;i<zero_length;i++){
            nbcdStr.append(0000);
        }
        for(int i=1;i<length;i++){//把负号跳过
            nbcdStr.append(CharTo4bit(decimalStr.charAt(i)));
        }
    }
    return nbcdStr.toString();
}

四、 NBCD（符号位用4位表示）转化成十进制整数的真值

1. 4位二进制转 1位十进制：bit4ToChar

从左到右，累加
num=num*2+(bit4.charAt(i)-‘0’);

public static String bit4ToChar(String bit4){
    int num=0;
    for(int i=0;i<4;i++){
        num=num*2+(bit4.charAt(i)-'0');
    }
    return String.valueOf(num);
}

步骤

初始化一个 StringBuilder 用于构建十进制字符串。
从第4位开始，每4位表示一个十进制数字，使用 bit4ToChar 方法将其转换为对应的十进制字符，并添加到 StringBuilder 中。
去除前面多余的0（保留至少一位，以满足数为0）。
将 StringBuilder 转换为字符串，并解析为整数。
根据符号位确定结果是否为负数。
返回十进制字符串。

完整代码

public static String NBCDToDecimal(String NBCDStr) {
    int num=0;
    StringBuilder num_sb=new StringBuilder();   //初始化 StringBuilder
    for(int i = 4;i<32;i+=4){       //转换每个4位二进制数字
        num_sb.append(bit4ToChar(NBCDStr.substring(i,i+4)));
    }
    //去除前面多余的0（留一位，以满足数为0）
    int length=num_sb.length();
    int count=0;
    while (num_sb.charAt(0)=='0'&&length!=1){       //去除前面多余的0(留1位)
        num_sb.deleteCharAt(0);
        length=num_sb.length();
    }
    String demical = new String(num_sb);
    num=Integer.parseInt(demical);      //解析为整数
    if (NBCDStr.substring(0, 4).equals("1101")){    //负数判断
        num=-num;
    }
    demical=String.valueOf(num);        //转为字符串
    return demical;
}

// 将4位二进制字符串转换为对应的十进制字符
public static char bit4ToChar(String binStr) {
    int num = 0;
    for (int i = 0; i < 4; i++) {
        num = num * 2 + (binStr.charAt(i) - '0');
    }
    return (char) (num + '0');
}

五、将浮点数真值转化成32位单精度浮点数表示

特殊

如果8位指数位全为0, 就代表当前数是个非规格数. 或者说, 形如 * 00000000 *********************** 格式的数就是非规格数.
- 用于表示0, 以及非常靠近0的数, 比如1E-38.
- 非规格数的实际指数固定为-126
如果8位指数位全为1, 就代表当前数是个特殊数. 或者说, 形如 * 11111111 *********************** 格式的数就是特殊数.
- 无穷大和NaN

1. 0

1
2
3

if (num == 0.0f) {
    return "00000000000000000000000000000000";
}

2.NaN

符号位：0或1
指数位：11111111
尾数位：任意非零值（通常为10000000000000000000000）

一般表示用：0 11111111 10000000000000000000000

1
2
3

if (Float.isNaN(num)) {
    return "01111111110000000000000000000000";
}

3. 无穷大

8位指数位全为1：11111111
23位尾数位全为0：00000000000000000000000

正无穷：01111111100000000000000000000000
负无穷：11111111100000000000000000000000

if (num == Float.POSITIVE_INFINITY){
    return "+Inf";
}else if(num<=Float.NEGATIVE_INFINITY){
    return "-Inf";
}

4. 非规格数

步骤：

特殊情况处理
1. 零
2. 正负无穷：num == Float.POSITIVE_INFINITY
3. NaN: if (Float.isNaN(num))
正常情况处理
1. 正负
2. 调整尾数到1.f~2.f范围：（指数初始为0）
  - 尾数偏大时，除以2，指数加1。while (num >= 2.0f)
  - 尾数偏小时，乘以2，指数减1。while (num < 1.0f && exponent > -126)
    - 如果指数减小到了-126，则非规格化数！
3. 规格化判断
  - 非规格化数：如果实际指数为-126，则指数部分全为0，尾数不变（已经小于1.0f了）。
  - 规格化数：尾数减去1.0f，指数加偏移量127。
4. 构建IEEE 754二进制字符串：
  - 符号位：1位
  - 指数位：8位——除二取余法
  - 尾数位：23位——乘二减一法：
    - 如果乘二之后大于1.0f，则1；否则0。
    - 先出现的在左！

完整代码

public static String floatToBinary(String floatStr) {
       float num = Float.parseFloat(floatStr);
       //1、0
       if(num==0){
           String zeroStr="00000000000000000000000000000000";
           return zeroStr;
       }
       //2.+Inf和-Inf（正负无穷）
       if (num == Float.POSITIVE_INFINITY){
           return "+Inf";
       }else if(num<=Float.NEGATIVE_INFINITY){
           return "-Inf";
       }
       //3.NaN
       if(Float.isNaN(num)){
           return "01111111110000000000000000000000";
       }else if(Float.isNaN(-num)){
           return "11111111110000000000000000000000";
       }
       //4. 正常情况
       //4.1判断正负
       boolean is_neg=false;
       if(num<0){
           is_neg=true;
       }

       int exponent=0;//指数
       //尾数
       int offset=127;;//偏移量

       //4.2 调整尾数到1.f~2.f范围
       if(num<0){
           num=-num;
       }
       while (num>=2.0f){   //尾数偏大
           num/=2.0f;
           exponent++;
       }
       while (num<1.0f&&exponent>-126){    //尾数偏小
           num*=2.0f;
           exponent--;
       }
       //4.3 规格化判断
       if (exponent <=-126) {
           exponent = 0; // 非规格化数，指数部分全为0(实际指数固定为-126)
       } else {
           num -= 1.0f; // 规格化数，尾数减去1
           exponent += offset; // 加偏移量
       }
       //4.4 化为IEEE
       StringBuilder binFloat=new StringBuilder();
       //符号位
       if (is_neg){
           binFloat.append("1");
       }else {
           binFloat.append("0");
       }
       //指数位
       char[] exp = new char[8];
       for(int i=7;i>=0;i--){
           if(exponent%2==1){
               exp[i]='1';
           }else{
               exp[i]='0';
           }
           exponent/=2;
       }
       //尾数位
       char[]wei=new char[23];
       for(int i=0;i<23;i++){
           num*=2.0f;
           if(num>=1.0f){
               wei[i]='1';
               num-=1.0f;
           }else{
               wei[i]='0';
           }
       }

       String expStr = new String(exp);
       String weiStr=new String(wei);
       binFloat.append(expStr);
       binFloat.append(weiStr);
       return binFloat.toString();
   }

六、32位单精度浮点数表示转化成浮点数真值

1. 特殊情况

//1. 0
        if(binStr=="00000000000000000000000000000000"){
            Float zero = 0.0f;
            return String.valueOf(zero);
        }
        //2. NaN
        if(binStr=="01111111110000000000000000000000"){
           Float nan = Float.NaN;
           return String.valueOf(nan);
        }
        //3. 正负无穷
        if(binStr=="01111111100000000000000000000000"){
           Float pos_inf=Float.POSITIVE_INFINITY;
           return String.valueOf(pos_inf);
        }else if(binStr=="11111111100000000000000000000000"){
            Float neg_inf=Float.NEGATIVE_INFINITY;
            return String.valueOf(neg_inf);
        }

2. 正常情况（规格化数+非规格化数）

符号位
指数位
- 提取指数位的8位二进制数，并转换为整数。
- 对于规格化数，减去偏移量127。
- 对于非规格化数（指数位等于0），实际指数为-126。
尾数位：
- 提取尾数位的23位二进制数，并转换为浮点数。
- 对于规格化数，尾数部分隐含一个1。规格化数，加1.0f
计算浮点数值：
- 根据指数调整尾数的值/直接算（注意double和float的转换）
  - float num=weishu(float)Math.pow(2,exponent);*
- 如果符号位为1，则结果为负数。

完整代码

    public static String binaryToFloat(String binStr) {
        //1. 0
        if(binStr=="00000000000000000000000000000000"){
            Float zero = 0.0f;
            return String.valueOf(zero);
        }
        //2. NaN
        if(binStr=="01111111110000000000000000000000"){
           Float nan = Float.NaN;
           return String.valueOf(nan);
        }
        //3. 正负无穷
        if(binStr=="01111111100000000000000000000000"){
           Float pos_inf=Float.POSITIVE_INFINITY;
           return String.valueOf(pos_inf);
        }else if(binStr=="11111111100000000000000000000000"){
            Float neg_inf=Float.NEGATIVE_INFINITY;
            return String.valueOf(neg_inf);
        }
        //4. 正常情况
        //4.1 正负
        boolean is_neg=false;
        if(binStr.charAt(0)=='1'){
            is_neg=true;
        }
        //4.2指数
        int exponent=0;
        for(int i=0;i<8;i++){
            exponent=exponent*2+(binStr.charAt(i+1)-'0');
        }
        if(exponent!=0){
            exponent-=127;//规格数
        }else{
            exponent=-126;//非规格数
        }
        //4.3 尾数
        float weishu=0.0f;
        float Add = 0.5f;
        for(int i=9;i<32;i++){
            if(binStr.charAt(i)=='1'){
                weishu+=Add;
            }
            Add/=2.0f;
        }
        if (exponent!=-126){//规格化数，加1.0f
            weishu+=1.0f;
        }
        //5.计算
        while (exponent>0){
            weishu*=2.0f;
            exponent--;
        }
        while (exponent<0){
            weishu/=2.0f;
            exponent++;
        }
        if(is_neg){
            weishu=-weishu;
        }
        //法2：直接算
//        float num=weishu*(float)Math.pow(2,exponent);
//        if (is_neg){
//            num=-num;
//        }
        return String.valueOf(weishu);
    }

1-十进制二进制浮点数转换

Universe Hamster

一、十进制整数->二进制补码

1. 用2整除的方式（正数）

2. 负数转化为其补码——（其绝对值转化成二进制后）逐位取反+加一

3. 将字符数组转换为字符串

步骤

完整代码：

二、二进制补码->十进制整数

错误方法-无法通过最大/最小值测试

1.逐位累加（！！从左边开始！！）

2. char转int

3. 处理负数

步骤：

完整代码

总结：二进制补码和十进制整数相互转换：

三、十进制整数的真值转化成NBCD

1. NBCD

2.将单位十进制数字转化为4位二进制形式

3. 步骤

4. 【注意】语法

完整代码

四、 NBCD（符号位用4位表示）转化成十进制整数的真值

1. 4位二进制 转 1位十进制：bit4ToChar

步骤

完整代码

五、将浮点数真值转化成32位单精度浮点数表示

特殊

1. 0

2.NaN

3. 无穷大

4. 非规格数

步骤：

完整代码

六、32位单精度浮点数表示转化成浮点数真值

1. 特殊情况

2. 正常情况（规格化数+非规格化数）

完整代码

Other Articles

2-补码加减乘除

Hello World

1. 4位二进制转 1位十进制：bit4ToChar